DDPM: Denoising Diffusion Probabilistic Models
논문: https://arxiv.org/abs/2006.11239
Diffusion model은 데이터에 여러 step에 걸쳐 random noise를 추가해 noise data를 만들고, 그 역방향으로 가는 확률분포를 학습해서 데이터를 생성하고자한다.
Forward(Diffusion) process

Data distribution인 q에서 sample된 x0들이 있을 때 gaussian distribution의 noise를 T step 동안 추가하며 x1, x2, ..., xT를 생성하는 forward process의 분포는 아래와 같이 정의된다.

이렇게 표시할 수 있는 이유는 diffusion model의 확률분포는 바로 전 상태에만 영향을 받는 markov chain의 성질을 갖기 때문이다.

이때 q(x_t | x_t-1)은 아래와 같이 정의된다.

여기서 beta는 noise를 주기위한 variance schedule이며 t가 커질수록 증가한다.
beta는 0~1 사이의 아주 작은 수로 설정하는데, 위 수식의 의미는 기존 x_t-1을 대부분 반영하고, beta_t만큼 약간의 noise를 반영해서 x_t를 만들겠다는 의도이다. (scale 유지)
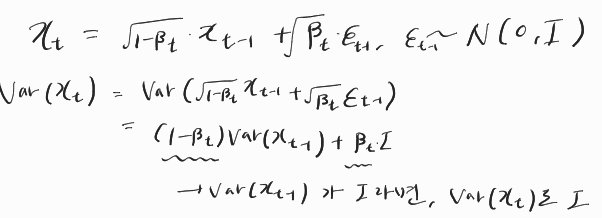
forward process에서는 아래와 같은 reparameterization trick을 사용해서 유용한 성질을 유도할 수 있다.

따라서 계산의 편의를 위해 alpha를 아래와 같이 정의하면
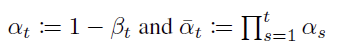
xt를 이렇게 표현할 수 있고,

xt-1을 계속 전개하다보면 아래와 같이 x0로 표현가능하다.

즉, 중간 과정 없이 x0로부터 xt를 바로 구할 수 있는 분포를 알 수 있게 된다.

Reverse(denoising) process

forward process의 반대인 q(x_t-1 | x_t) 를 알 수 있다면 단순히 저 분포에서 sampling하여 noise를 제거하여 image를 생성할 수 있을 것이다. 하지만 저걸 구하기 위해서는 모든 dataset이 있어야하기에 구할 수가 없다. 따라서 이를 근사하기 위해 갖고 있는 data를 기반으로 likelihood가 제일 높은 p_θ를 찾아내는 것이다. 다행인 점은 beta가 아주 작을 때, q(x_t | x_t-1)이 가우시안 분포를 따른다면 그의 반대인 q(x_t-1 | x_t)도 가우시안 분포를 따른 다는 사실이 증명되었다고 한다. 따라서 이를 근사하는 p_θ(x_t-1 | x_t)역시 가우시안 분포를 따른다고 가정할 수 있다.

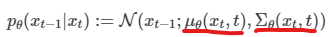
reverse process 역시 forward와 마찬가지로 markov chain 특성이 있기에 위의 식과 같이 p(x_t-1 | x_t)의 곱으로 표현이 가능하고(p(x_T) ~ N(0, I)), p는 가우시안을 따르기 때문에 우리는 xt, t가 주어졌을 때의 평균과 분산만을 알아내면 reverse process를 할 수 있는 model을 얻는 것과 같다. (DDPM에서는 σ_θ 를 상수로 두어 mean만 구하면 되도록 한다.)
위에서 우리가 알고 싶었던 q(x_t-1 | x_t)는 알 수 없지만 x0가 주어졌을 때의 q(x_t-1 | x_t, x_0)는 알 수 있다.


Loss
확률분포 q에서 뽑은 x0들이 있을 때, 이 x0를 가장 뽑을 것 같은 확률분포 p_θ를 찾아내는 것이 목표이다. 즉 데이터가 주어졌을 때 데이터를 뽑을 확률인 likelihood를 최대화 하여 가장 그 데이터들을 뽑을 것 같은 확률분포를 찾아내는 것이다.
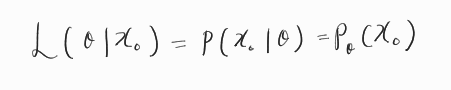
하지만 계산의 편의를 위해 log를 취하고 -를 붙여 minimize하도록 변경하여 negative log likelihood를 최소화하는 문제로 변경하여 loss를 설정한다.

이 식을 위에서 구한 q, p를 사용하 아래와 같이 전개하고



최종적으로 3개의 loss term으로 정리할 수 있다.

DDPM Loss
Diffusion model의 loss term 세가지는 다음과 같은 의미를 가지며, DDPM에서는 이들을 간소화하여 loss를 간단하게 만드는 트릭을 사용한다.
1. L_T term (regularization term)

이 텀은 q(xT | x0)의 분포가 가우시안 분포(p(xT))를 따르도록 beta를 학습하게 해주는 term이다. 하지만 DDPM에서 beta는 상수이므로 이 term에서 학습되는 parameter는 없다. 따라서 loss term에서 사용할 필요가 없다. (1000번의 step으로 q(xT|x0)는 충분히 가우시안 분포와 유사하다.)
2. L_t-1 term (t > 1) (denoising term)

t번째 image가 주어졌을 때 t-1의 분포를 p_θ가 q와 근접하도록 하는 term이다. q(x_t-1 | x_t)는 구할 수 없으므로 data를 기반으로 한 q(x_t-1 | x_t, x_0)를 근사하도록 θ를 조절해 p_θ를 q와 유사하게 만든다.
KL divergence의 두 factor가 가우시안 분포를 따를 경우 아래와 같이 간소화된 형태로 구할 수 있다.

이를 활용해 중간의 평균값의 차이를 기준으로 L_t-1을 정리하면

위의 식을 얻을 수 있다. μ_틸다는 q(x_t-1 | x_t, x_0)의 평균이고, μ_θ는 학습할 p(x_t-1 | x_t)의 평균이다. 계수로 붙은 분산은,

위 식의 분산에 해당하는데 DDPM에서는 이 값을 loss의 간소화를 위해 상수로 둔다. (forward process에서 추가된 noise(분산)를 알고 있으니 backward process에서 빠질 분산도 이를 기반으로 할 것이다라는 가정)

두 가지의 경우로 실험해 봤는데 결과는 비슷하다고 한다.
다시 L_t-1 수식으로 돌아와서,

forward process에서 구했던 μ_틸다에

q(xt | x0)의 특성을 이용해 x0를 대입하면

위와 같이 μ_틸다를 x0, ϵ의 식으로 표현할 수 있다.
L_t-1를 보면 μ_θ는 μ_틸다와 같도록 해야 loss가 0이기 때문에, x_t가 주어졌을 때 μ_틸다를 예측해야한다.
이 때 μ_틸다에서 변수는 ϵ 뿐이기 때문에 μ_θ를 다음과 같이 정의할 수 있다.
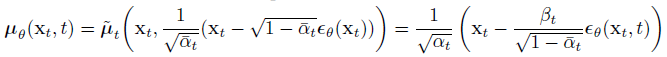
L_t-1에 μ_θ는 μ_틸다를 대입해서 정리하면

이렇게 변경할 수 있고 앞의 계수는 상수이기 때문에(DDPM에서 분산 역시 상수로 취급) 무시할 수 있고 최종적으로

이런 형태의 loss로 변경할 수 있다.
3. L_0 term (reconstruction term)

pθ(x0 | x1)는 아래의 식을 따른다.

하지만 실제로 x0는 [0, 255]로 이루어진 discrete image를 [-1, 1] 범위로 scaling한 것이다. 즉, 이산분포를 따라야한다. 심지어 분포로만 알고 있어도 됐던(KLD로 분포의 차이만 계산한다던가) pθ(x_t-1 | x_t) (t > 1)과 다르게 L0 term에서는 실제로 pθ(x0 | x1)의 확률값을 구해야하기 때문에 위의 수식을 활용하여 pθ(x0 | x1)가 따르는 이산 분포를 정의해야한다. 그 정의는 아래의 식과 같다.

먼저, x0가 속하지 않는 [-1, 1] 범위를 벗어나는 값의 확률은 각 edge case인 pixel 값이 -1, 1인 pixel의 확률로 넣는다. 정상적인 pixel 값에 대한 확률은 [x0 - 1/255, x0 + 1/255] 범위의 확률로 구한다. 그렇게 함으로써 x0_i가 [-1, -1 + 2/255, -1 + 4/255, ..., 1 - 2/255, 1]인 이산 분포를 구해낸다.
(pixel 단위가 아닌 x0 image의 확률은 각 x0_i pixel의 확률을 별도로 계산하여 곱해서 구한다.)

integral 안쪽의 term은 위 그림의 초록색 적분 값(위에는 검정색 라인)이지만, 2/255가 작은 값이니 범위에 따른 높이 차를 고려하지 않고(적분하지 않고) 높이가 정규 분포의 f(x)값, 너비가 2/255로 생각(초록색 사각형)하여 아래와 같이 계산할 수 있다.

DDPM에서는 p_θ 의 분산을 learnable하지 않은 상수로 취급했기 때문에 앞의 계수 term은 무시해도 되고, 따라서 L_t-1에서 t가 1일 때와 L_0의 term이 같아진다. 따라서, L_t-1 (t>1)을 L_t-1 (t>0)으로 변경하면서 L_0 term을 L_t-1으로 통합시킬 수 있게된다.
Simple loss
최종적으로 3개의 loss term으로 구성되었던 loss가 아래와 같이 단순화된다.

즉, step t와 x0를 input으로 받아 ϵ만을 예측하는 모델을 학습하면 되는 것이다.

하나의 iteration에서 uniform random t와, gaussian random ϵ를 사용해 image batch의 loss를 구해 학습한다.

아래 세개의 식에 의해 x_t-1을 x_t, t를 가지고 계산해 낼 수 있게 된다.(σ는 미리 정의 된 상수)


$$ x_{t-1} = \mu_{\theta }(x_{t}, t) + \sigma _{t} \cdot \epsilon $$
추론된 마지막 x0는 training data x0와 달리[-1, 1] 범위의 값이 아니지만 이를 [0, 255]로 scaling해서 이미지로 만든다.
