ResNet: Deep Residual Learning for Image Recognition (CVPR 2016)

 

 

 

논문: https://arxiv.org/abs/1512.03385

Deep Residual Learning for Image Recognition

 

Microsoft에서 발표한 residual(잔차) 학습을 활용한 ResNet 논문에 대한 리뷰이다.

 

0. Abstract

 

 Input이 들어오면 그 값을 바탕으로 output을 만들어내는 일반적인 layer(unreferenced (to input data) function)와 다르게 구조의 변경을 통해 redisual과 input data 그 자체를 참조하여 학습하도록 만들었다. 여기서 residual은 잔차, 오차 등으로 불릴 수 있으며 plain layer(구조 변경하기 전)의 optimal output과 input의 차이를 말한다. 이런 구조변경을 통해 152개의 layer를 쌓아 VGG보다 8배나 깊은 모델을 덜 복잡하고, 더 정확하게 학습할 수 있었다. 이는 Imagenet dataset 뿐만 아니라 CIFAR-10와 같이 작은 규모의 데이터셋에서도 효과적이었다.

 

 

1. Introduction

 

 Deep learning에서 layer가 더 많이 쌓일수록 다양한 feature를 반영할수 있다는 다양한 연구가 존재해왔으며 layer의 depth가 중요하다는 사실은 계속해서 대두되었다.

 

 

 하지만 depth를 단순하게 늘리는 것이 간단하게 모델의 성능으로 귀결되지는 않는다. 여기에는 두 가지 문제가 존재한다.

첫 번째로는 Vanishing/Explodinf gradients 현상이 있다. 하지만 이 문제는 normalization을 통해 해결할 수 있었다.

 

 

두 번째 문제는 Degradation problem (accuracy ↓)으로, depth가 깊어짐에 따라 정확도가 수렴하다가 빠르게 떨어지는 현상을 말하는데 이게 해결되지 않은 문제였다.

 

 한번 "구조적으로" 생각해보자. 잘 학습된 얕은 모델의 layer의 가중치를 그대로 가져오고, 중간중간 identity mapping layer(input과 output이 같은 layer)를 껴 넣어 더 깊은 모델을 구성한다면 당연히 모델의 output이 같으니 training error는 증가하지 않을 것이다. 하지만 실험적인 결과는 달랐다. 지금까지 나온 방법들로는 이러한 구조를 갖는 모델을 학습시키기 어려웠고 오히려 accuracy가 떨어졌다.

 

 저자들은 이  문제를 해결하기 위해 residual을 학습하는 구조를 생각해냈다. 원래 학습하고자 했던 target function H를 학습하기 어려우니 H block의 residual인 H(x) - x를 output으로 하는 F를 대신 학습하려는 것이다. 정의에 따라 F(x) = H(x) - x 가 성립하고 다시말해 H(x) = F(x) + x가 된다. 즉, 원래 학습하고자 했던 target function을 잔차를 학습한 layer F + input 으로 변경할 수 있게 된다.

 이러한 구조로 변경한 이유는 F를 학습하는 것이  H를 학습하는 것보다 쉬울 것이라고 생각했기 때문이다. Deep한 구조를 갖게되면 optimal model은 identity mapping layers와 유사한 hidden layers를 많이 갖고 있을 것이라 예상할 수 있는데(아래 실험에서 증명함), stacked nonlinear layers로 identity mapping을 학습하는 것은 쉽지 않은 일이다. 하지만 H가 identity mapping와 유사함에 따라 F는 zero mapping에 유사하게 되고 zero mapping을 학습하는 것은 비교적 간단한 일이된다.

 다시말해, reconstruction을 함으로써 학습해야 하는 대상이 학습하기 어려운 identity mapping에서 학습하기 쉬운 zero mapping으로 변경되는 것이다.

 

 

 

2. Related Work

Residual Representations

 VLAD, Fisher Vector 라는 애들도 residual vector로 encoding해서 효과를 봤었고 Multigrid method, Hierarchical basis preconditioning도 scale에 대한 residual을 활용해서 빠른 converge를 할 수 있었다더라.

 

Shortcut Connections

 

  Shortcut connection도 오랫동안 연구된 내용인데 (Inception의 1x1 conv branch도 그렇고) 저자가 제안한 방식은 parameter를 추가로 사용하지 않고 그렇기 때문에 shortcut이 적용되지 않을 일도 없어서 좋다고 함.

 

3. Deep Residual Learning

3.1 Residual Learning

 Introduction에서 한 얘기와 유사한 내용이다. Multiple nonlinear layers가 어떤 복잡한 target function H를 점진적으로 근사할 수 있다는 것은 F: H(x) - x 도 마찬가지로 근사할 수 있다는 말이다. 그러니 우리는 H말고 F를 학습하도록 할 것이다. 이게 더 학습하기 쉬우니까.

 

 Degradation 현상을 보면서 의문은 시작됐다. 잘 학습된 shallow model에 identity mapping만 추가된 구조는 분명 training error가 더 커지지 않을 것이다. 하지만 현존하는 solver들로 구현해보니 실제로는 증가했다. 저자는 이 이유가 identity mapping을 하도록 학습하는 것이 multiple nonlinear layers에게는 어려운 일이기 때문일 것이라고 생각했다. 그렇기 때문에 residual을 학습하도록 구조를 변경하고 identity보다 쉬운 zero mapping을 학습하게 했다(identity 라는 것은 residual이 0이라는 말이니까).

 

 

 물론 실제로는 optimal이 identity mapping은 아닐테지만 identity mapping과 유사할 것이라 생각할 수 있고(직관적으로 layer가 많아질수록 각 layer를 통과했을 때 값이 많이 바뀌기보다 미세하게 변경될 것으로 생각할 수 있다. 깊은 모델일 수록 미세조정하는 hidden layer가 많을 것. 뿐만 아니라 Fig7에서 학습 이후에 residual layer의 response가 0에 가깝다는 것을 실험적으로 증명하였다.) 이는 reformulation이 문제를 해결하기 위한 좋은 전제조건이라 할 수 있다. 왜냐하면 ResNet은 HE initialization(~N(0, (2/n)^(1/2)))으로 weight를 설정하기 때문에 초기값이 0에 가깝고, 따라서 0에 가까운 optimal redisual에 쉽게 수렴할 수 있는 것이다.

 

 

3.2 Identity Mapping by Shortcuts

 

 Shortcut x는 residual function F의 output과 element wise로 합쳐진다. 단순한 덧셈이 추가된 것이기 때문에 parameter가 추가되지 않고 계산의 복잡성도 크게 증가하지 않는다. shortcut을 적용하지 않은 plain 모델과 element wise addition을 제외하고는 완전히 동일하기 때문에 같은 기준에서 비교하기 좋다. shortcut을 적용하다보면 가로지르는 layer에서 filter의 수(channel)가 많아져 input x의 차원이 변경되는 경우가 발생하는데 이런 경우에는 x와 F(x)의 차원이 달라져 element wise addition을 할 수 없다. 이런 경우에는 projection matrix W_x를 사용해 x의 차원을 F(x)에 맞춘 뒤 더할 수 있다. 하지만 projection하지 않아도 degradation 문제를 해결하기 충분하기 떄문에 차원이 일치하는 경우에는 굳이 사용하지 않는다.

 

3.3 Network Architectures

 

Plan Network

VGG에서 영감을 받았고 conv layer는 3x3을 사용한다. output feature map size가 같은 layer들은 filter의 수도 같게하고, feature map size가 반감될 때는 filter의 수를 두배로 늘려 각 layer의 complexity를 같게했다. 흥미로운 내용은 맨 처음부터 stride 2로 conv layer를 적용해서 feature map size를 바로 반으로 줄이고 시작한다는 점이고 후반부에는 GoogLeNet처럼 GAP, FC, Softmax로 결과를 뽑는다. 주목할만한 점은 34 layer로 구성했지만 19 layer VGG에 비해 겨우 18% 밖에 연산량이 되지 않게 했다 (같은 feature map size에서 사용하는 filter 수가 더 적음).

 

Residual Network

Plain net에서 shortcut만 추가해서 redidual을 학습하도록 했을 뿐이다. 다만 3.2에 언급한대로 차원이 달라지는 경우가 존재하는데 이 때는 (A) 추가된 filter를 0으로 채우거나, (B) 1x1 conv로 projection해서 차원을 맞추거나 하는 방법을 사용했다. 두 방법 모두 stride를 2로 해서 feature map을 줄였다(feature map의 홀수번째 cell은 버려졌다는 얘기).

 

4. Experiments

4.1 ImageNet Classification

 

 

Plane Networks

plain net의 경우에는 34 layer가 18 layer에 비해 전체적으로 더 높은 training error가 발생했다. 그 이유는 vanishing gradient 때문은 아니었다 (gradatation problem이다).

 

Residual Networks

 반면 resnet으로 실험했을 때는 세가지 포인트가 있었다.

1. deep하게 해도 성능이 좋다. (shallow res vs deep res)
2. plain net에 비해 성능이 좋다. (plain vs res)
3. converge가 빠르다. (깊지 않은 모델이어도)

 

Identity vs Projection Shortcuts

Shortcut의 차원이 달라져야할 때 세 가지 방법(A, B, C)에 대한 실험결과이다. A < B < C 순으로 결과가 좋았지만 차이는 크지 않았으며 이 차이는 degradation 문제와는 크게 상관이 없었다. C의 경우 모든 shortcut에서 projection을 하기 때문에 시공간적으로 비효율적이라 고려하지 않기로 했고, A방법이 추가적인 parameter를 사용하지 않는 사실이 bottleneck architecture(후술)에서 특히 효과적이라는 점은 중요한 포인트이.

 

Deeper Bottleneck Architectures

34 layer 이상으로 deep한 모델을 구성하기 위해 학습 시간을 고려해서 보다 효율적인 residual function F의 구조를 고안했다. 앞뒤로 1x1 conv를 붙여 차원을 줄이고 늘리며 가운데에는 3x3 conv layer를 둔다. 이는 layer를 더 deep하게 (34 -> 50) 만들지만 time complexity는 비슷하다.

• Left: 3*3*64*56*56*64 + 3*3*64*56*56*64 = 231,211,008
• Right: 1*1*256*56*56*64 + 3*3*64*56*56*64 + 1*1*64*56*56*256 = 218,365,952
• (kernel * kernel * channel_in * H * W * channel_out)

Bottleneck 구조로 변경하면 shortcut projection 비용이 훨씬 증가하기 때문에 identity shortcut이 bottlenect 구조에서 더 효율적이다.

• Left: 1*1*64*56*56*64 = 12,845,056
• Right: 1*1*256*56*56*256 = 205,520,896 (shortcut 비용이 거의 F function만큼이다)

 

4.2 CIFAR-10 and Analysis

 

ImageNet dataset 뿐만 아니라 CIFAR-10 dataset을 대상으로도 실험해보았다. Fig.3에 있는 모델을 약간 변형한 형태이며 여기서도 plain net과 resnet의 차이는 shortcut만 있게하고 비교했다. 왼쪽 표에서처럼 plain net은 depth가 깊어질수록 성능이 감소했고 110 layer는 60%이상 에러로 전혀 동작하지 않았다. 반면에 resnet은 110 layer까지도 depth에 비례하게 성능이 좋아지는 것을 확인할 수 있었다.

 

Analysis of Layer Responses

 

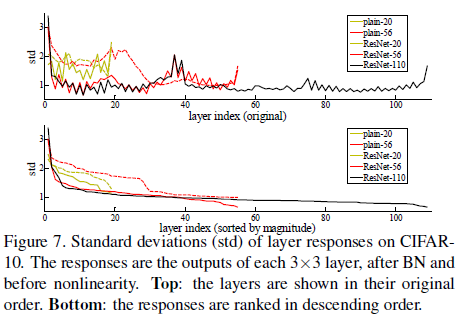
위 표의 y축 값은 학습된 resnet layer의 response strenth이다(output이 잔차라서 표준편차가 response strength라 할 수 있음). 3.1에서 예상한것처럼 identity mapping이 많아 resnet의 response는 plain에 비해 0에 가까웠고, 깊어짐에 따라 identity mapping이 더 많아져 zerro mapping을 하는 layer가 더 많아진 것을 확인할 수 있었다. 즉 깊어짐에 따라 각각의 layer는 input x에 대한 변경을 조금만 가하는 것이었다.

 

극단적으로 layer를 1000개로 늘려봤을 때 degradation 문제 없이 training error를 감소하는 것을 볼 수 있었다. 하지만 test error는 training error와 다르게 110 layer보다 성능이 떨어졌다(그래도 꽤 준수한 성능이긴 했다). 저자는 이를 CIFAR-10 dataset에 비해 모델이 너무 복잡해서 발생하는 overfitting 때문이라고 주장한다. 추가적인 정규화를 통해 이것 역시 좋게 할 수 있을 것이라고..